Janaka Raagas Explained

As discussed in the article (Concept of Raaga)..there are 72 Janaka Raagas. Also as discussed in the article, there is a systematic way to name these ragas. Now let us look at the how these 72 Raagas were arrived at. Why are there 72 raagas? Why not less and why not more? Math enthusiasts, you definitely need to read through…

As mentioned in the article (Swaras ), there are 12 unique Swaras.

Here are the basic rules of Janaka Raaga – A complete Raaga –

1. It is complete. It has all the seven notes. The Aarohana is the ascending order interpretation and Avarohana is the descending order interpretation.
2. Each Swara is unique and has a higher value than the previous note in the Arohana and vice versa in the avarohana.

With these basic rules, let us come up with the basic format of the Janaka Raaga. There is also a higher Sa at the end of Aarohana and at the beginning of Avarohana.

We know that there are 7 unique Swaras, so here are the eight empty slots (including a slot for the higher Sa).

Aarohana
Avarohana

 

Let us know fill the easiest ones, the constants that never change. Sa and Pa.  

Aarohana	Sa				Pa			Sa
Avarohana	Sa			Pa				Sa

Pictorially this is how it looks:

Getting to the Madhyamas:

The next important step is to fill the Ma. This is simpler as we know that there are only 2 types of Ma- Shuddha Madhyama or Ma1 and Prati Madhyama Ma2. Also Ma is not equivalent to any other notes, so it is unique. 

Aarohana	Sa			Ma1	Pa			Sa
Avarohana	Sa			Pa	Ma1			Sa

 

Aarohana	Sa			Ma2	Pa			Sa
Avarohana	Sa			Pa	Ma2			Sa

 

All the Janaka Raagas can hence be broadly classified as Shuddha Madhyama Raagas (first group) and Prati Madhyama Raagas (second group).

Here is a pictorial representation of the same.

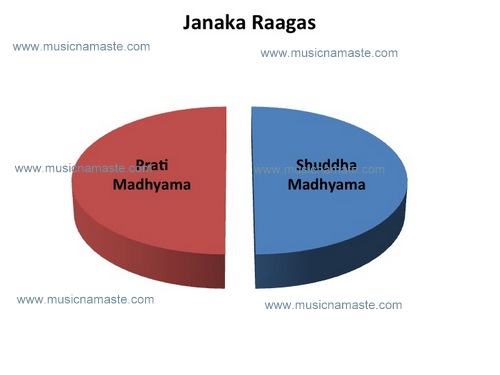
Getting to the Rishabhas and Gandharas

The note higher to Sa has to be Ri. But which one, there are 3 of them Shuddha Ri ( Ri1), Chatushruti Rishabha ( Ri2 ) or Shatshruti Rishabha ( Ri3 )?

Here are the possibilities:

Sa-Ri1
Sa-Ri2
Sa-Ri3

And similarly the third spot is 1 of 3 types of Ga. : Shuddha Gandhara (Ga1), Sadharana Gandhara (Ga2), Antara Gandhara( Ga3).

So here are possibilities:

Sa-Ri1-Ga1
Sa-Ri1-Ga2
Sa-Ri1-Ga3

Sa-Ri2-Ga1
Sa-Ri2-Ga2
Sa-Ri2-Ga3

Sa-Ri3-Ga1
Sa-Ri3-Ga2
Sa-Ri3-Ga3

But we know that

• Ri2 = Ga1
• Ri3=Ga2
• Ri3 > Ga1

Hence the basic rule of one swara greater than than the prior needs to be satisfied. So eliminating the redundancies, we get the following 6 arrangements:

Sa-Ri1-Ga1
Sa-Ri1-Ga2
Sa-Ri1-Ga3

Sa-Ri2-Ga2
Sa-Ri2-Ga3

Sa-Ri3-Ga3

So now let us fill up the empty slots for the Ma1 Group:

Aarohana	Sa	Ri1	Ga1	Ma1	Pa			Sa
Avarohana	Sa			Pa	Ma1	Ga1	Ri1	Sa

 

Aarohana	Sa	Ri1	Ga2	Ma1	Pa			Sa
Avarohana	Sa			Pa	Ma1	Ga2	Ri1	Sa

 

Aarohana	Sa	Ri3	Ga3	Ma1	Pa			Sa
Avarohana	Sa			Pa	Ma1	Ga3	Ri1	Sa

 

Aarohana	Sa	Ri2	Ga2	Ma1	Pa			Sa
Avarohana	Sa			Pa	Ma1	Ga2	Ri2	Sa

 

Aarohana	Sa	Ri2	Ga3	Ma1	Pa			Sa
Avarohana	Sa			Pa	Ma1	Ga3	Ri2	Sa

 

Aarohana	Sa	Ri3	Ga3	Ma1	Pa			Sa
Avarohana	Sa			Pa	Ma1	Ga3	Ri3	Sa

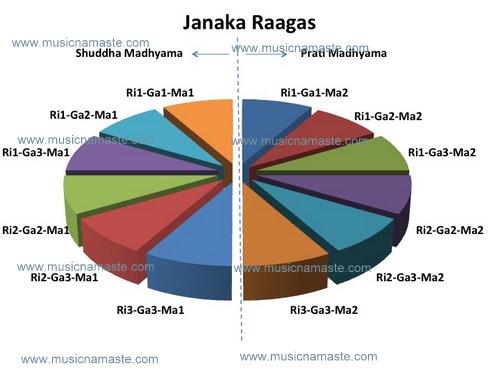
Getting to the Daivatas and Nishaadas

For easy elaboration, consider the first Ri1 Ga1 Ma1 Group.

The arrangements of Da and Ni are as follows:

Sa-Ri1-Ga1-Ma1-Da1-Ni1

Sa-Ri1-Ga1-Ma1-Da1-Ni2

Sa-Ri1-Ga1-Ma1-Da1-Ni3

Sa-Ri1-Ga1-Ma1-Da2-Ni1

Sa-Ri1-Ga1-Ma1-Da2-Ni2

Sa-Ri1-Ga1-Ma1-Da2-Ni3

Sa-Ri1-Ga1-Ma1-Da3-Ni1

Sa-Ri1-Ga1-Ma1-Da3-Ni2

Sa-Ri1-Ga1-Ma1-Da3-Ni3

But we know that

• Da2 = Ni1

• Da3=Ni2

• Da3 > Ni1

Hence the basic rule of one swara greater than than the prior needs to be satisfied. So eliminating the redundancies, we get the following 6 arrangements:

Sa-Ri1-Ga1-Ma1-Da1-Ni1

Sa-Ri1-Ga1-Ma1-Da1-Ni2

Sa-Ri1-Ga1-Ma1-Da1-Ni3

Sa-Ri1-Ga1-Ma1-Da2-Ni2

Sa-Ri1-Ga1-Ma1-Da2-Ni3

 

Sa-Ri1-Ga1-Ma1-Da3-Ni3

So for the R1G1 group we get the following 6 arrangements for Da and Ni.

Aarohana	Sa	Ri1	Ga1	Ma1	Pa	Da1	Ni1	Sa
Avarohana	Sa	Ni1	Da1	Pa	Ma1	Ga1	Ri1	Sa

 

Aarohana	Sa	Ri1	Ga1	Ma1	Pa	Da1	Ni2	Sa
Avarohana	Sa	Ni2	Da1	Pa	Ma1	Ga1	Ri1	Sa

 

Aarohana	Sa	Ri1	Ga1	Ma1	Pa	Da1	Ni3	Sa
Avarohana	Sa	Ni3	Da1	Pa	Ma1	Ga1	Ri1	Sa

  

Aarohana	Sa	Ri1	Ga1	Ma1	Pa	Da2	Ni2	Sa
Avarohana	Sa	Ni2	Da2	Pa	Ma1	Ga1	Ri1	Sa

 

Aarohana	Sa	Ri1	Ga1	Ma1	Pa	Da2	Ni3	Sa
Avarohana	Sa	Ni3	Da2	Pa	Ma1	Ga1	Ri1	Sa

  

Aarohana	Sa	Ri1	Ga1	Ma1	Pa	Da3	Ni3	Sa
Avarohana	Sa	Ni3	Da3	Pa	Ma1	Ga1	Ri1	Sa

 

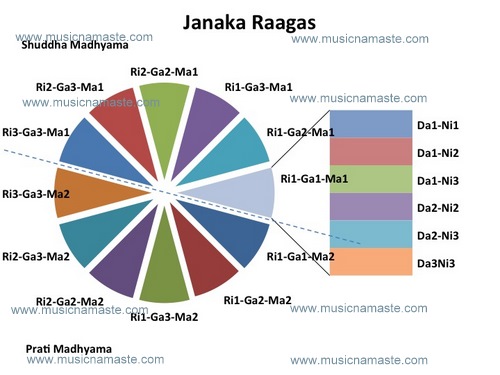
This completes the elaboration of Ri1 Ga1 Ma1 group, which along with Da and Nis gave another 6 Raagas. In this fashion, we can work out the Raagas for all the 6 Ri Ga Ma1 groups, which will total to 6 X 6 =36 Raagas.

The table below enumerates the 36 Shuddha Madhyama Raagas. Only Aarohana is listed for easy reading. The Avarohana is the same notes in the reverse order.

Note how the Raagas have been  numbered accordingly. This number is the Melakarta Number of the Raaga.

Melakarta #	Aarohana
1	Sa	Ri1	Ga1	Ma1	Pa	Da1	Ni 1	Sa
2	Sa	Ri1	Ga1	Ma1	Pa	Da1	Ni 2	Sa
3	Sa	Ri1	Ga1	Ma1	Pa	Da1	Ni 3	Sa
4	Sa	Ri1	Ga1	Ma1	Pa	Da2	Ni 2	Sa
5	Sa	Ri1	Ga1	Ma1	Pa	Da2	Ni 3	Sa
6	Sa	Ri1	Ga1	Ma1	Pa	Da3	Ni 3	Sa
7	Sa	Ri1	Ga2	Ma1	Pa	Da1	Ni 1	Sa
8	Sa	Ri1	Ga2	Ma1	Pa	Da1	Ni 2	Sa
9	Sa	Ri1	Ga2	Ma1	Pa	Da1	Ni 3	Sa
10	Sa	Ri1	Ga2	Ma1	Pa	Da2	Ni 2	Sa
11	Sa	Ri1	Ga2	Ma1	Pa	Da2	Ni 3	Sa
12	Sa	Ri1	Ga2	Ma1	Pa	Da3	Ni 3	Sa
13	Sa	Ri1	Ga3	Ma1	Pa	Da1	Ni 1	Sa
14	Sa	Ri1	Ga3	Ma1	Pa	Da1	Ni 2	Sa
15	Sa	Ri1	Ga3	Ma1	Pa	Da1	Ni 3	Sa
16	Sa	Ri1	Ga3	Ma1	Pa	Da2	Ni 2	Sa
17	Sa	Ri1	Ga3	Ma1	Pa	Da2	Ni 3	Sa
18	Sa	Ri1	Ga3	Ma1	Pa	Da3	Ni 3	Sa
19	Sa	Ri2	Ga2	Ma1	Pa	Da1	Ni 1	Sa
20	Sa	Ri2	Ga2	Ma1	Pa	Da1	Ni 2	Sa
21	Sa	Ri2	Ga2	Ma1	Pa	Da1	Ni 3	Sa
22	Sa	Ri2	Ga2	Ma1	Pa	Da2	Ni 2	Sa
23	Sa	Ri2	Ga2	Ma1	Pa	Da2	Ni 3	Sa
24	Sa	Ri2	Ga2	Ma1	Pa	Da3	Ni 3	Sa
25	Sa	Ri2	Ga3	Ma1	Pa	Da1	Ni 1	Sa
26	Sa	Ri2	Ga3	Ma1	Pa	Da1	Ni 2	Sa
27	Sa	Ri2	Ga3	Ma1	Pa	Da1	Ni 3	Sa
28	Sa	Ri2	Ga3	Ma1	Pa	Da2	Ni 2	Sa
29	Sa	Ri2	Ga3	Ma1	Pa	Da2	Ni 3	Sa
30	Sa	Ri2	Ga3	Ma1	Pa	Da3	Ni 3	Sa
31	Sa	Ri3	Ga3	Ma1	Pa	Da1	Ni 1	Sa
32	Sa	Ri3	Ga3	Ma1	Pa	Da1	Ni 2	Sa
33	Sa	Ri3	Ga3	Ma1	Pa	Da1	Ni 3	Sa
34	Sa	Ri3	Ga3	Ma1	Pa	Da2	Ni 2	Sa
35	Sa	Ri3	Ga3	Ma1	Pa	Da2	Ni 3	Sa
36	Sa	Ri3	Ga3	Ma1	Pa	Da3	Ni 3	Sa

 

Similarly Ma2 group will give 36 Raagas. The total number of Melakarta Raagas is hence 72.

Here are the 36 Prati Madhyama Melakarta Raagas.

Melakarta #	Aarohana
37	Sa	Ri1	Ga1	Ma2	Pa	Da1	Ni 1	Sa
38	Sa	Ri1	Ga1	Ma2	Pa	Da1	Ni 2	Sa
39	Sa	Ri1	Ga1	Ma2	Pa	Da1	Ni 3	Sa
40	Sa	Ri1	Ga1	Ma2	Pa	Da2	Ni 2	Sa
41	Sa	Ri1	Ga1	Ma2	Pa	Da2	Ni 3	Sa
42	Sa	Ri1	Ga1	Ma2	Pa	Da3	Ni 3	Sa
43	Sa	Ri1	Ga2	Ma2	Pa	Da1	Ni 1	Sa
44	Sa	Ri1	Ga2	Ma2	Pa	Da1	Ni 2	Sa
45	Sa	Ri1	Ga2	Ma2	Pa	Da1	Ni 3	Sa
46	Sa	Ri1	Ga2	Ma2	Pa	Da2	Ni 2	Sa
47	Sa	Ri1	Ga2	Ma2	Pa	Da2	Ni 3	Sa
48	Sa	Ri1	Ga2	Ma2	Pa	Da3	Ni 3	Sa
49	Sa	Ri1	Ga3	Ma2	Pa	Da1	Ni 1	Sa
50	Sa	Ri1	Ga3	Ma2	Pa	Da1	Ni 2	Sa
51	Sa	Ri1	Ga3	Ma2	Pa	Da1	Ni 3	Sa
52	Sa	Ri1	Ga3	Ma2	Pa	Da2	Ni 2	Sa
53	Sa	Ri1	Ga3	Ma2	Pa	Da2	Ni 3	Sa
54	Sa	Ri1	Ga3	Ma2	Pa	Da3	Ni 3	Sa
55	Sa	Ri2	Ga2	Ma2	Pa	Da1	Ni 1	Sa
56	Sa	Ri2	Ga2	Ma2	Pa	Da1	Ni 2	Sa
57	Sa	Ri2	Ga2	Ma2	Pa	Da1	Ni 3	Sa
58	Sa	Ri2	Ga2	Ma2	Pa	Da2	Ni 2	Sa
59	Sa	Ri2	Ga2	Ma2	Pa	Da2	Ni 3	Sa
60	Sa	Ri2	Ga2	Ma2	Pa	Da3	Ni 3	Sa
61	Sa	Ri2	Ga3	Ma2	Pa	Da1	Ni 1	Sa
62	Sa	Ri2	Ga3	Ma2	Pa	Da1	Ni 2	Sa
63	Sa	Ri2	Ga3	Ma2	Pa	Da1	Ni 3	Sa
64	Sa	Ri2	Ga3	Ma2	Pa	Da2	Ni 2	Sa
65	Sa	Ri2	Ga3	Ma2	Pa	Da2	Ni 3	Sa
66	Sa	Ri2	Ga3	Ma2	Pa	Da3	Ni 3	Sa
67	Sa	Ri3	Ga3	Ma2	Pa	Da1	Ni 1	Sa
68	Sa	Ri3	Ga3	Ma2	Pa	Da1	Ni 2	Sa
69	Sa	Ri3	Ga3	Ma2	Pa	Da1	Ni 3	Sa
70	Sa	Ri3	Ga3	Ma2	Pa	Da2	Ni 2	Sa
71	Sa	Ri3	Ga3	Ma2	Pa	Da2	Ni 3	Sa
72	Sa	Ri3	Ga3	Ma2	Pa	Da3	Ni 3	Sa

 

Must Read: How are the Raagas Named